2020重庆选调生排列组合模型题解题思路

【导读】华图选调生招聘考试网辽宁分校发布：2020重庆选调生排列组合模型题解题思路，详细信息请阅读下文！更多资讯请关注华图微信公众号(huatuv)，欢迎加入全国选调生备考交流群：1079603880。

排列组合问题是行测数量关系科目中的高频题型，而相比其他题型，难度较大，也是广大考生最为头疼的难点题型之一。

一、考察题量

根据表1“2015-2019年国家公务员考试排列组合题目出题数量”可知，排列组合每年至少1题，无论是副省级考试还是地市级考试均会有所涉及。

表1 2015-2019年国家公务员考试排列组合题目出题数量

数量关系	2019	2019	2018	2018	2017	2017	2016	2016	2015	2015
	副省	地市	副省	地市	副省	地市	副省	地市	副省	地市
题量	1	1	1	1	1	1	1	1	2	2

二、基本原理

1、分类与分步

分类是指对完成一件事，需要划分几个类别，各类别内方法可以独立完成该事;

分步是指对完成一件事，需要分为几个步骤，每个步骤内的方法只能保证完成该步。

2、加法原理与乘法原理

加法原理：分类完成的事件，完成该事件的各类别方法总数相加。

乘法原理：分步完成的事件，将完成该事件的各步骤的方法直接相乘。

3、基本公式：

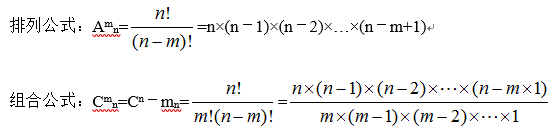
三、常考题型

1、基础公式型

【例】从甲地到乙地每天有直达班车4班，从甲地到丙地每天有直达班车5班，从丙地到乙地每天有直达班车3班，则从甲地到乙地共有( )不同的乘车法。

A. 12种

B. 19种

C. 32种

D. 60种

【答案】B

【解题思路】从甲地到乙地有两种不同路线：

(1)直达4种;

(2)根据乘法原理，从甲地先到丙地再到乙地，共5×3=15种。

因此不同的乘车方法，运用加法原理，共有4+15=19(种)。答案选择B。

2、分步排列组合

(2019-联考-61.)某小学组织6个年级的学生外出参观包括A科技馆在内的6个科技馆，每个年级任选一个科技馆参观，则有且只有两个年级选择A科技馆的方案共有：

A. 1800种

B. 18750种

C. 3800种

D. 9375种

【答案】D

【解题思路】

第一步，有且只有两个年级选择A科技馆，有C=15(种)方案;第二步，剩下的4个年级，每个年级都有除了A科技馆以外的剩余5个科技馆可选，有54=625(种)方案。最后运用乘法原理，共有15×625=9375(种)方案。因此，选择D选项。

【拓展】最终答案尾数为5，可用尾数法确定答案，只有D选项满足。

3、分类排列组合

(2018-广西-54.)单位3个科室分别有7名、9名和6名职工。现抽调2名来自不同科室的职工参加调研活动，问有多少种不同的挑选方式?

A. 146

B. 159

C. 179

D. 286

【答案】B

【解题思路】设3个科室分别为A、B、C科室，那么挑两个科室、每个科室挑1人的情况分为以下3类：

①从A、B里挑，有7×9=63种方式;

②从B、C里挑，有9×6=54种方式;

③从A、C里挑，有7×6=42种方式。

因此，共有63+54+42=159种方式(可使用尾数法)。因此，选择B选项。

4、逆向思维

逆向计算：正面情况较多的排列组合，反面情况往往较少，则可用总数减去反面情况数。

(2019-黑龙江-62.)某企业从10名高级管理人员中选出3人参加国际会议。在10名高级管理人员中，有一线生产经验的有6人，有研发经验的有5人，另有2人既无一线生产经验也无研发经验。如果要求选出的人中，具备一线生产经验的人和具备研发经验的人都必须有，问有多少种不同的选择方式?

A. 96 B. 100

C. 106 D. 112

【答案】C

【解题思路】由题意，同时具备一线生产经验和具备研发经验的人为6+5+2-10=3，则该企业只具备一线生产经验的人为6-3=3，只具备研发经验的人为5-3=2，则满足题意要求的情况=总情况-只具备一线生产经验的情况-只具备研发经验的情况=C-C-C·C-C·C-C·C-C·C=106。因此，选择C选项。

四、特殊模型

1、捆绑型

捆绑型：如果题目要求一部分元素必须在一起，可先将要求在一起的部分进行排序，然后视为一个整体，再与其他元素一起进行排列。

题目标志：必须相邻、必须相连、不能分开。

(2016-国家-68.)为加强机关文化建设，某市直机关在系统内举办演讲比赛，3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同参赛顺序的种数在以下哪个范围之内?

A. 大于20000

B. 5001~20000

C. 1000~5000

D. 小于1000

【答案】C

2、插空型

插空型：如果题目要求一部分元素不能在一起，则可先排列其他主体，然后把不能在一起的元素插空到已经排列好的元素中间。

题目标志：不能相邻、不能相连、必须分开

(2018-广东-29.)某条道路一侧共有20盏路灯。为了节约用电，计划只打开其中的10盏。但为了不影响行路安全，要求相邻的两盏路灯中至少有一盏是打开的，则共有( )种开灯方案。

A. 2

B. 6

C. 11

D. 13

【答案】C

 

 

3、隔板型Ⅰ-至少1个

隔板型：如果题目表述为一组相同的元素分成数量不等的若干组，要求每组至少一个元素，则将隔板插入元素之间，计算出分类总数。

 

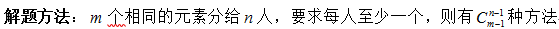
(2014-河南-36.)将7个大小相同的桔子分给4个小朋友，要求每个小朋友至少得到1个桔子，一共有几种分配方法?

A. 14 B. 18

C. 20 D. 22

【答案】C

4、隔板法Ⅱ-至少x个

隔板型-至少x个：如果题目表述为一组相同的元素分成数量不等的若干组，要求每组至少x个元素，则先分给每组x-1个，再将其转化为至少1个的题型。

(陕西2013-80)某领导要把20项任务分给三个下属，每个下属至少分得三项任务，则共有多少种不同的分配方式?

A.28 B.36

C.54 D.78

【答案】D

5、隔板法Ⅲ-至少0个

隔板型-至少0个：如果题目表述为一组相同的元素分成数量不等的若干组，要求每组至少0个元素，则先分给每组1个，再将其转化为至少1个的题型。

【例】将10个大小相同的桔子分给4个小朋友，要求每个小朋友至少得到0个桔子，一共有多少种分配方法?

A. 280 B. 284

C. 282 D. 286

【答案】D

6、重复剔除型

【例】将4个人平均分成2组，共有多少种分配方法?

AB+CD

AC+BD

AD+BC

BC+AD

BD+AC

CD+AB

解题方法：平均分组时，一旦有N个组人数相同，最后都要除以00000000000以避免重复情形。

(2017-江苏A-64.)某单位组织志愿者参加公益活动，有8名员工报名，其中2名员工超过50岁。现将他们分成3组，人数分别为3、3、2，要求2名超过50岁的员工不在同组，则不同的分组方案共有：

A. 120种 B. 150种

C. 160种 D. 210种

【答案】D

【解题思路】根据要求2名超过50岁的员工“不在”同组，分为以下2种情况：

 

 

共有90+120=210种。因此，选择D选项。

7、环形排列

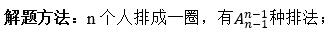
(2019-陕西-120.)主人随机安排10名客人坐成一圈就餐，这10名客人中有两对情侣，那么这两对情侣恰好都被安排相邻而坐的概率约在( )。

A.0到2%之间 B.2%到3%之间

C.3%到4%之间 D.4%到5%之间

E.5%到6%之间 F.6%到7%之间

G.7%到8%之间 H.8%以上

【答案】E

 

 

8、错位排列：

解题方法：有n封信和n个信封，每封信都不能装在自己的信封里，可能的方法的种数计作Dn，则，D1=0，D2=1，D3=2，D4=9，D5=44……000000000000种。

(2017-国家-70.)某集团企业5个分公司分别派出1人去集团总部参加培训，培训后再将5人随机分配到这5个分公司，每个分公司只分配1人。问5个参加培训的人中，有且仅有1人在培训后返回原分公司的概率：

A. 低于20% B. 在20%~30%之间

C. 在30%~35%之间 D. 大于35%

【答案】D

通过以上总结，大家可以发现，排列组合问题虽有一定的难度，但也是有规律可循的，希望上述总结，能为大家提供一些帮助，也希望大家平日能够掌握原理，多加练习，熟记公式，在考场中取得好成绩!

（编辑：liap）